波函数和薛定谔方程
波函数的统计解释
波函数是描述微观粒子的波,一个波函数描述一个粒子的状态(又称态)。波函数是空间与时间的函数,记作\(\varPsi(\boldsymbol{r},t)\)。其模的平方描述粒子某时刻在空间中某一点出现概率的相对大小。对波函数进行归一化后得到的波函数的模的平方描述粒子在某时刻空间中一点的概率大小,即
\[
\rho(\boldsymbol{r},t)=\left |\varPsi(\boldsymbol{r},t)\right |^2=\varPsi(\boldsymbol{r},t)\varPsi^*(\boldsymbol{r},t).
\]
当然,也存在无法归一化的波函数,这样波函数只能描述其相对概率。
特殊地,对于自由粒子(即势场关于空间的函数为常数),其波函数为
\[
\varPsi(\boldsymbol{r},t)=A\mathrm{e}^{\frac{\mathrm{i}}{\hbar}(\boldsymbol{p}\cdot\boldsymbol{r}-Et)},
\]
其中,\(\boldsymbol{p}\)为粒子动量,\(E\)为粒子的能量。
态叠加原理
如果\(\varPsi_1(\boldsymbol{r},t)\)和\(\varPsi_2(\boldsymbol{r},t)\)都是体系的可能状态,那么其线性组合\(c_1\varPsi_1(\boldsymbol{r},t)+c_2\Phi_2(\boldsymbol{r},t)\)也是体系的可能状态。更一般的,其可以描述为
\[
\varPsi=\sum_i^n c_n\varPsi_n.
\]
对于体系各种可能的动量\(\boldsymbol{p}\),任一波函数都可以写成不同动量的波函数之和,即
\[
\varPsi(\boldsymbol{r},t)=\int c(\boldsymbol{p},t)\varPsi_{\boldsymbol{p}}(\boldsymbol{r})\textrm{d}\boldsymbol{p}.
\]
其中:
\[
\varPsi_{\boldsymbol{p}}(\boldsymbol{r})=A\mathrm{e}^{\frac{\mathrm{i}}{\hbar}(\boldsymbol{p}\cdot\boldsymbol{r})}=\dfrac{1}{(2\pi \hbar)^{3/2}}\mathrm{e}^{\frac{\mathrm{i}}{\hbar}(\boldsymbol{p}\cdot\boldsymbol{r})}
\]
薛定谔方程
一般薛定谔方程
薛定谔方程的形式为:
\[
\mathrm{i}\hbar \dfrac{\partial \varPsi}{\partial t}=(-\dfrac{\hbar ^2}{2m}\nabla ^2+U(\boldsymbol{r},t))\varPsi.\tag{1}
\]
概率流密度
对薛定谔方程两边同时取共轭:
\[
-\mathrm{i}\hbar \dfrac{\partial \varPsi ^*}{\partial t}=(-\dfrac{\hbar ^2}{2m}\nabla ^2+U(\boldsymbol{r},t))\varPsi ^*.\tag{2}
\]
计算:\((1)\times\varPsi ^*-(2)\times\varPsi\),得到:
\[
\dfrac{\partial}{\partial t}\varPsi\varPsi^*=\dfrac{\mathrm{i}\hbar}{2m}\nabla(\varPsi\nabla\varPsi ^*-\varPsi ^*\nabla\varPsi).
\]
定义概率流密度:
\[
\boldsymbol{J}=\dfrac{\mathrm{i}\hbar}{2m}(\varPsi\nabla\varPsi ^*-\varPsi ^*\nabla\varPsi),
\]
于是
\[
\dfrac{\partial w}{\partial t}+\nabla \boldsymbol{J}=0.
\]
积分形式:
\[
\int _V\dfrac{\partial w}{\partial t}\textrm{d}V=-\oint_S \boldsymbol{J}\textrm{d}S.
\]
这说明,例子在某个空间区域出现的概率关于时间的变化等同于概率流密度流入或流出这个空间区域的大小。
定态薛定谔方程
对于势能不随时间变化的势场来说,波函数可以利用变量分离分离空间与时间项:
\[
\varPsi(r,t)=\psi(r)f(t).
\]
于是含时薛定谔方程可以变换成:
\[
\mathrm{i}\hbar f(t)\dfrac{\partial f(t)}{\partial t}=-\dfrac{\hbar ^2}{2m}\dfrac{1}{\psi(r)}\nabla ^2\psi (r)+U(r)=E.
\]
解得
\[
f(t)=C\mathrm{e}^{-\frac{\mathrm{i}E}{\hbar}t}.
\]
而空间项:
\[
\left [-\dfrac{\hbar ^2}{2m}\nabla ^2+U(r)\right ]\psi (r)=E\psi(r)
\]
由于方程不含时间,并且能量\(E\)是给定的,故称为定态薛定谔方程。
把\(-\dfrac{\hbar ^2}{2m}\nabla ^2+U(r)\)记作\(\hat{H}\),称为哈密顿算符,则定态薛定谔方程还可以简化成:
\[
\hat{H}\psi (r)=E\psi (r).
\]
对于不同的常数\(E_n\),都有不同的解\(\psi _n (r)\),则我们把\(E_n\)称为本征值,对应的\(\psi _n(r)\)称为本征函数。
定态问题的求解
对于已知的波函数初始状态\(\Psi(x,0)\),求解其定态问题一般通过如下方法:


关键在于对本征值与本征函数的求取,以及系数的确定问题。
自由粒子的本征函数中动量\(p\)与本征值\(E\)常满足以下关系:
\[
E=\dfrac{p^2}{2m}.
\]
若非自由粒子,则需要考虑哈密顿量\(\hat{H}\)中的势能项。
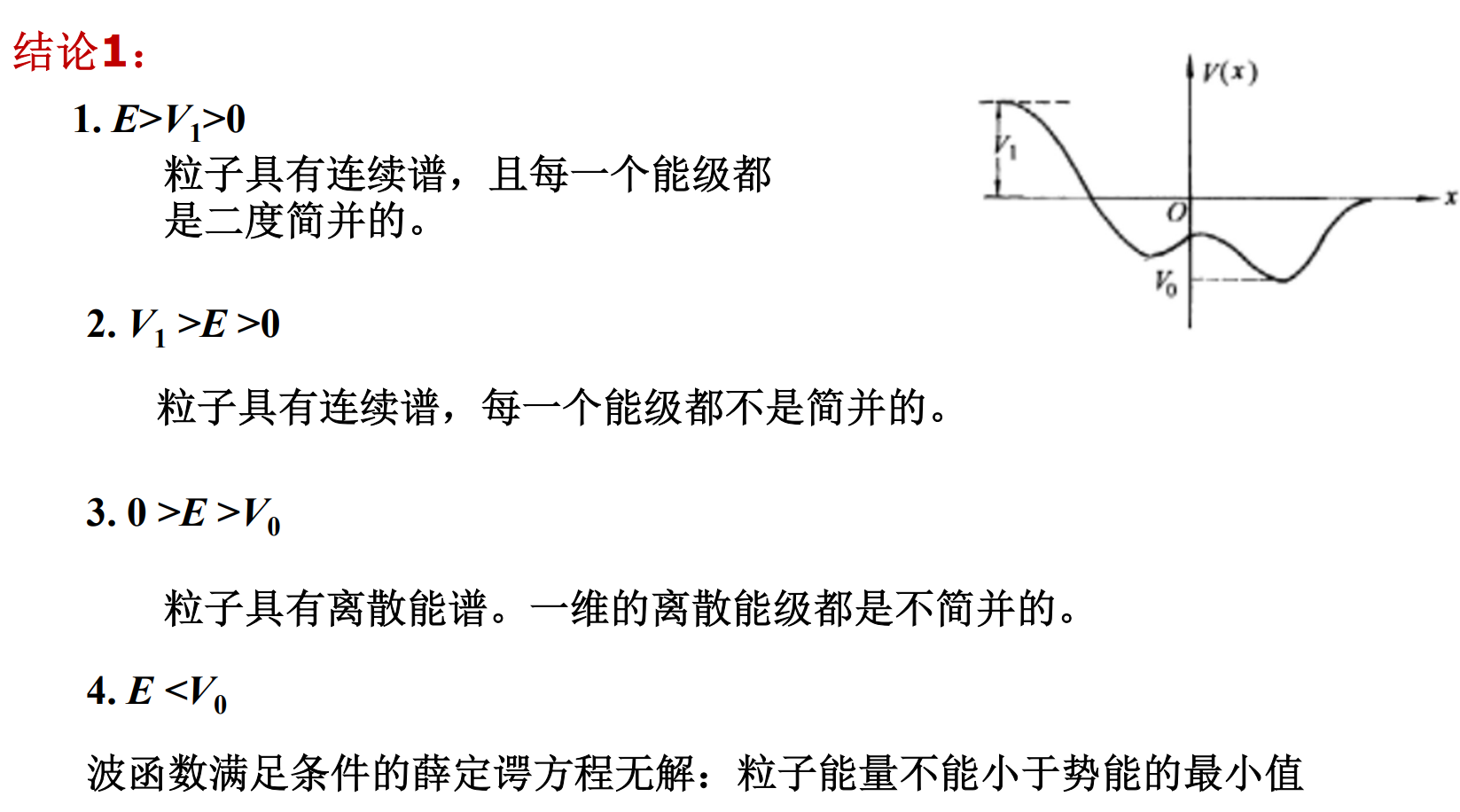
任意势场中粒子的波函数
结论

朗斯基行列式
对于两个函数\(\psi _1\)和\(\psi _2\),其朗斯基行列式定义为:
\[
W[\psi _1,\psi _2](x)=\begin{vmatrix}
\psi _1(x)&\psi _2(x)\\
\dfrac{\mathrm{d}\psi _1(x)}{\mathrm{d}x}&\dfrac{\mathrm{d}\psi _2(x)}{\mathrm{d}x}\\
\end{vmatrix}.
\]
如果两个函数的朗斯基行列式不为零,则证明它们线性无关。
最后更新:
March 12, 2023
创建日期:
March 12, 2023



