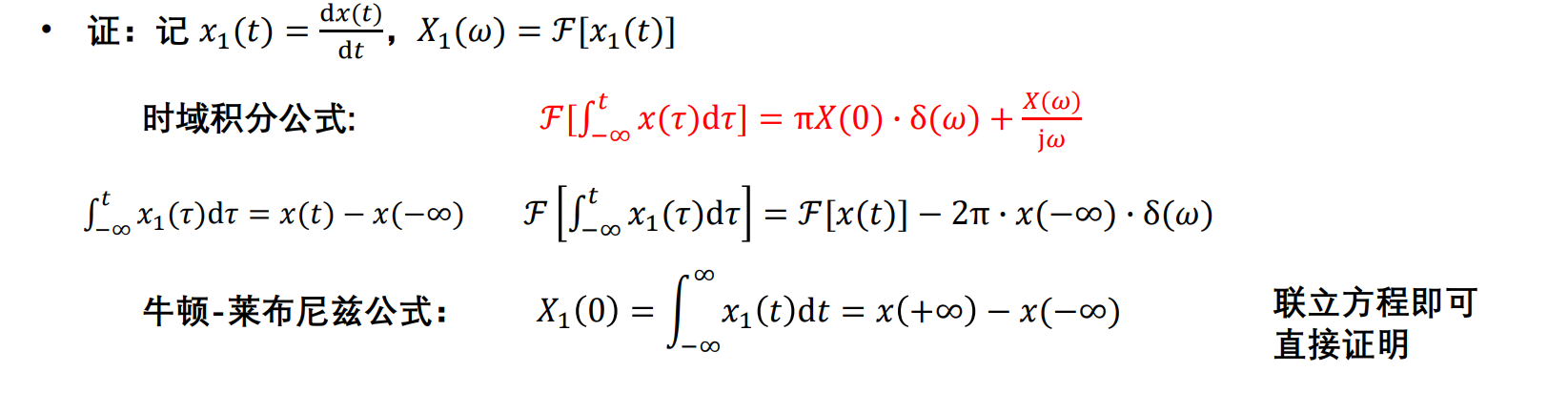非周期信号的频谱
傅里叶变换与反变换
定义
当周期\(T_1\to \infty\)时,其逐渐变为非周期信号。这种情况下,标准的傅里叶级数已经不再适用,此时引入频谱密度函数:
\[
F(\omega)=F(n\omega _1)T_1.
\]
其中\(T_1\to \infty\),于是可以得到傅里叶变换式:
\[
F(\omega)=\int_{-\infty}^{+\infty}f(t)\mathrm{e}^{-\mathrm{j}\omega t}\mathrm{d}t.
\]
这里强调\(F(\omega)\)一般是复变函数。
对于\(F(\omega)\),其可以通过傅里叶反变换得到\(F(t)\),即:
\[
f(t)=\dfrac{1}{2\pi}\int_{-\infty}^{+\infty}F(\omega)\mathrm{e}^{\mathrm{j}\omega t}\mathrm{d}t.
\]
满足上述变换式的一对函数\(f(t)\)和\(F(\omega)\)称为一对傅里叶变换对,记作\(f(t)\leftrightarrow F(\omega)\).并且信号需要满足绝对可积的条件才具有傅里叶变换。
常见的傅里叶变换对
门函数\(G_\tau (t)\)门高为\(E\)时,其傅里叶变换对:
\[
G_\tau (t)\leftrightarrow E\tau\cdot \mathrm{Sa}(\dfrac{\omega\tau}{2}).
\]
单边指数信号\(x(t)=\mathrm{e}^{-\alpha t}u(t)\)和双边指数信号\(x(t)=\mathrm{e}^{-\alpha \left | t \right |}\)的傅里叶变换对是:
\[
\mathrm{e}^{-\alpha t}u(t)\leftrightarrow \dfrac{1}{\alpha+\mathrm{j}\omega},
\]
\[
\mathrm{e}^{-\alpha \left | t \right |}\leftrightarrow \dfrac{2}{\alpha ^2+\omega ^2}.
\]
与冲激函数相关的傅里叶变换:
\[
\delta (t)\leftrightarrow 1,
\]
\[
\delta ^\prime (t)\leftrightarrow \mathrm{j}\omega.
\]
傅里叶变换的性质
线性性质
傅里叶变换具有线性性质。
时移性质
傅里叶变换具有时移性质。任一傅里叶变换对\(x(t)\leftrightarrow X(\omega)\),则\(x(t\pm t_0)\leftrightarrow X(\omega)\mathrm{e}^{\mathrm{j}\omega t_0}\).
傅里叶变换具有奇偶虚实性。任一傅里叶变换对\(x(t)\leftrightarrow X(\omega)\),则\(x(-t)\leftrightarrow X(-\omega)\),且\(x^*(t)\leftrightarrow X^*(-\omega)\).


时域微积分
时域微积分性质:若\(x(t)\leftrightarrow X(\omega)\),则
\[
\dfrac{\mathrm{d}}{\mathrm{d}t}x(t)\leftrightarrow \mathrm{j}\omega X(\omega).
\]
推广有:
\[
\dfrac{\mathrm{d}^n}{\mathrm{d}t^n}x(t)\leftrightarrow (\mathrm{j}\omega)^n X(\omega).
\]
时域积分时,情况有所不同,表示为:
\[
\mathcal{F}\left[\int_{-\infty}^{t}f(\tau)\mathrm{d}\tau \right]=\pi X(0)\delta(\omega)+\dfrac{X(\omega)}{\mathrm{j}\omega}.
\]
原函数\(x(t)\),当其导数\(x^\prime(t)\)的傅里叶变换更容易求得时,可以利用:
\[
X(\omega)=\mathcal{F}\left[ x(t)\right ]=\dfrac{1}{\mathrm{j}\omega}\mathcal{F}\left[ \dfrac{\mathrm{d}x(t)}{\mathrm{d}t} \right]+\pi [x(+\infty)+x(-\infty)]\delta(\omega).
\]
证明如下:
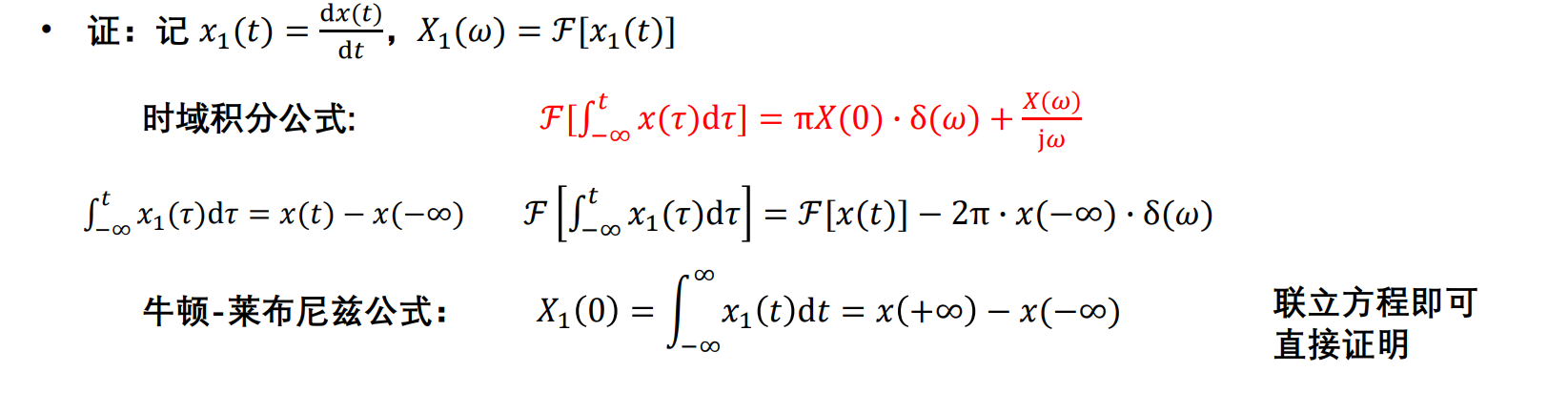
尺度变换
时移与尺度变换:
\[
x(at)\leftrightarrow \dfrac{1}{|a|}X(\dfrac{\omega}{a}),
\]
\[
x(at-t_0)\leftrightarrow \dfrac{1}{|a|}X(\dfrac{\omega }{a})\mathrm{e}^{\pm \mathrm{j}\frac{\omega t_0}{a}}.
\]
对偶性质
对偶性:如果\(x(t)\leftrightarrow X(\omega)\),则\(X(t)\leftrightarrow 2\pi x(-\omega)\).
频域微积分
若\(x(t)\leftrightarrow X(\omega)\),则有\(tx(t)\leftrightarrow \mathrm{j}\dfrac{\mathrm{d}}{\mathrm{d}\omega}X(\omega)\).
值得注意的是,左半部分\(tx(t)\)中的两个\(t\)并没有理论上的关系,也就是说,两者不需要保持相同的形式。
频移变换性质
对于一对傅里叶变换对\(x(t)\leftrightarrow X(\omega)\),有
\[
\mathrm{e}^{\mp \mathrm{j}\omega_0 t}x(t)\leftrightarrow X(\omega \pm \omega _0).
\]
注意,这里正负号对应关系是相反的(正对应负,负对应正)。
卷积性质
若\(x_1(t)\leftrightarrow X_1(\omega)\)且\(x_2(t)\leftrightarrow X_2(\omega)\),则:
\[
x_1(t)*x_2(t)\leftrightarrow X_1(\omega)X_2(\omega),
\]
和
\[
x_1(t)x_2(t)\leftrightarrow \dfrac{1}{2\pi }\left[X_1(\omega)*X_2(\omega)\right].
\]
多项式函数的傅里叶变换
由于\(\delta (t)\leftrightarrow 1\),并且结合对偶性,有\(1\leftrightarrow 2\pi\delta(\omega)\).再结合频域微积分:有
\[
t^n\leftrightarrow 2\pi (\mathrm{j}\dfrac{\mathrm{d}}{\mathrm{d}\omega })^n\delta (\omega).
\]
周期信号的傅里叶变换
若\(x_T(t)\)表示周期为\(T\)的信号,则其可以表示成为傅里叶展开式:
\[
x_T(t)=\sum_{n=-\infty}^{+\infty}X(n\omega _0)\mathrm{e}^{\mathrm{j}n\omega _0t}.
\]
对两边同时取傅里叶变换得到:
\[
X_T(\omega)=\sum_{n=-\infty}^{+\infty}X(n\omega _0)\cdot 2\pi\delta(\omega -n\omega _0).
\]
其中:
\[
X(n\omega _0)=\dfrac{1}{T}\int_{T}x(t)\mathrm{e}^{-\mathrm{j}n\omega_0 t}\mathrm{d}t=\dfrac{1}{T}X_0(\omega)\bigg |_{\omega =n\omega _0}.
\]
上述中,\(X_0(\omega)\)是\(x_T(t)\)取单周期内的信号作傅里叶变换得到的式子。
比较常用的是周期为\(T\)的单位冲激信号\(\delta_T(t)\)的傅里叶变换:
\[
\delta _T(t)=\omega _0\delta _{\omega _0}(\omega).
\]
其中,\(\omega _0=\dfrac{2\pi }{T}\).
最后更新:
March 31, 2023
创建日期:
March 31, 2023