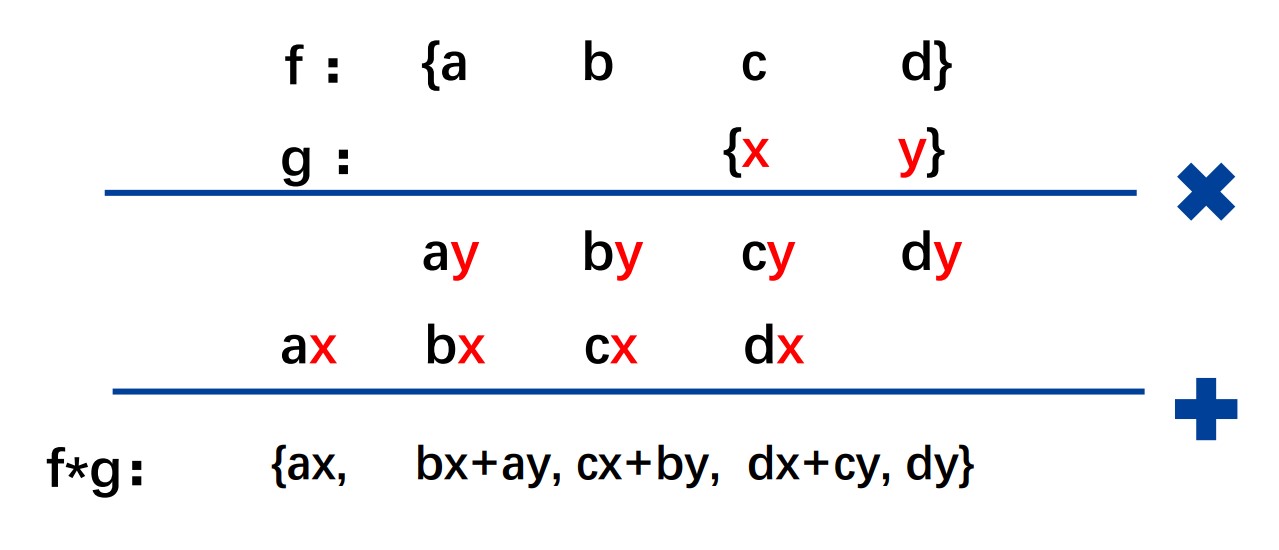跳转至

线性时不变系统的时域分析⚓︎

单位样值响应⚓︎

对于任一的信号激励，我们可以将其分解为若干个冲激函数的组合：

\[ \begin{cases} x[n]=\displaystyle\sum_{k=-\infty}^{+\infty}x[k]\delta [n-k]\quad &\text{离散情形}\\ x(t)=\displaystyle\int_{-\infty}^{+\infty}x(\tau)\delta (t-\tau)\ \mathrm{d} \tau\quad &\text{连续情形} \end{cases} \]

则输出可以表示成：

\[ \begin{cases} y[n]=\displaystyle\sum_{k=-\infty}^{+\infty}x[k]h [n-k]\quad &\text{离散情形}\\ y(t)=\displaystyle\int_{-\infty}^{+\infty}x(\tau)h (t-\tau)\ \mathrm{d} \tau\quad &\text{连续情形} \end{cases} \]

所以我们只要研究针对于激励\(\delta (t)\)的相应\(h(t)\)就可以得到任意输入所对应的输出了。

卷积和⚓︎

上面提到的\(y[n]=\displaystyle\sum_{k=-\infty}^{+\infty}x[k]h [n-k]\)我们称为卷积和。计算卷积和，一般可以从如下角度考虑：

缩小求和范围⚓︎

上述式子中对于\((-\infty,+\infty)\)的求和是难以计算的，但是，如果信号\(x[n]\)或者\(h[n]\)或者两者皆是因果信号，则卷积和可以缩小求和上下限。

考虑：\(k<0\)，则\(x[k]=0\)；\(k>n\)，则\(h[n-k]=0\)。于是卷积和可以化简为：

\[ y[n]=\displaystyle\sum_{k=-\infty}^{+\infty}x[k]h [n-k]=\displaystyle\sum_{k=0}^{n}x[k]h [n-k]. \]

图解法⚓︎

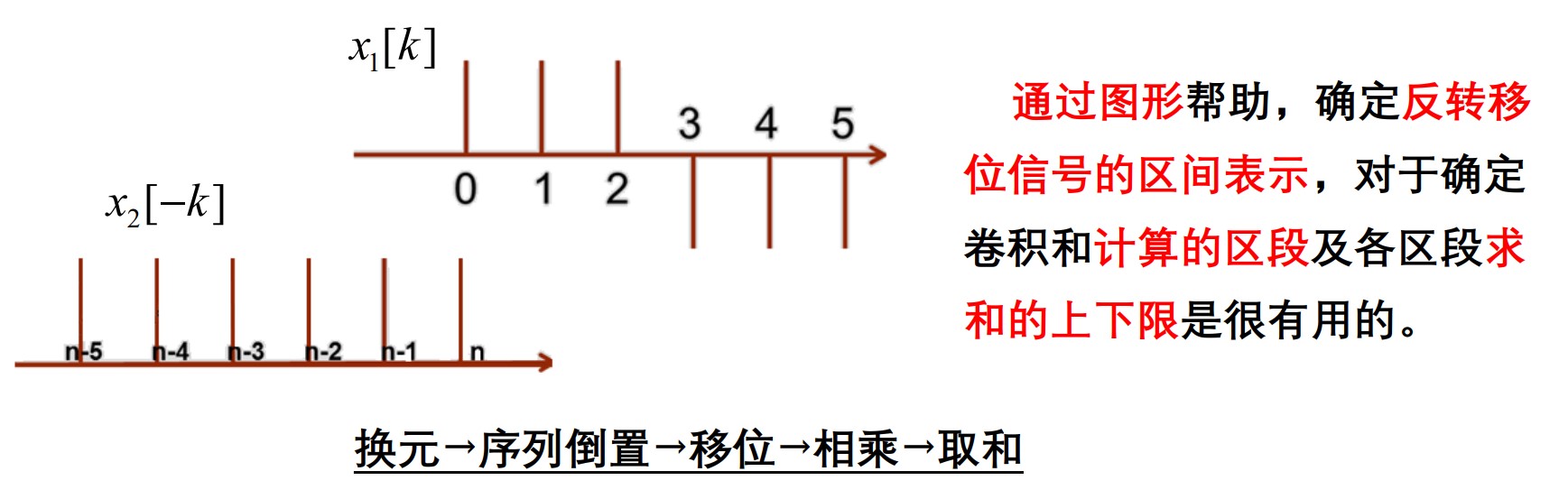
一种求离散序列卷积的方法就是图解法，见下图。

对于序列\(x_2[n]\)，先作倒置操作，即关于纵轴翻折。得到序列\(x_2[-k]\)。而后，开始求取给定\(n\)的值时卷积序列中\(y[n]\)的值：将\(x_2[-k]\)向右移动\(n\)步，得到\(x_2[n-k]\)。然后针对上下重合的部分取乘积再求和，得到的值就是\(y[n]\)。

不进位乘法⚓︎

对于离散序列的卷积，最好的方法就是不进位乘法。

对于序列\(x_1[n]\)和\(x_2[n]\)，进行不进位的乘法，得到的结果序列就是卷积结果。

卷积积分⚓︎

上面提到的\(y(t)=\displaystyle\int_{-\infty}^{+\infty}x(\tau)h (t-\tau)\ \mathrm{d} \tau\)我们就称为卷积积分。

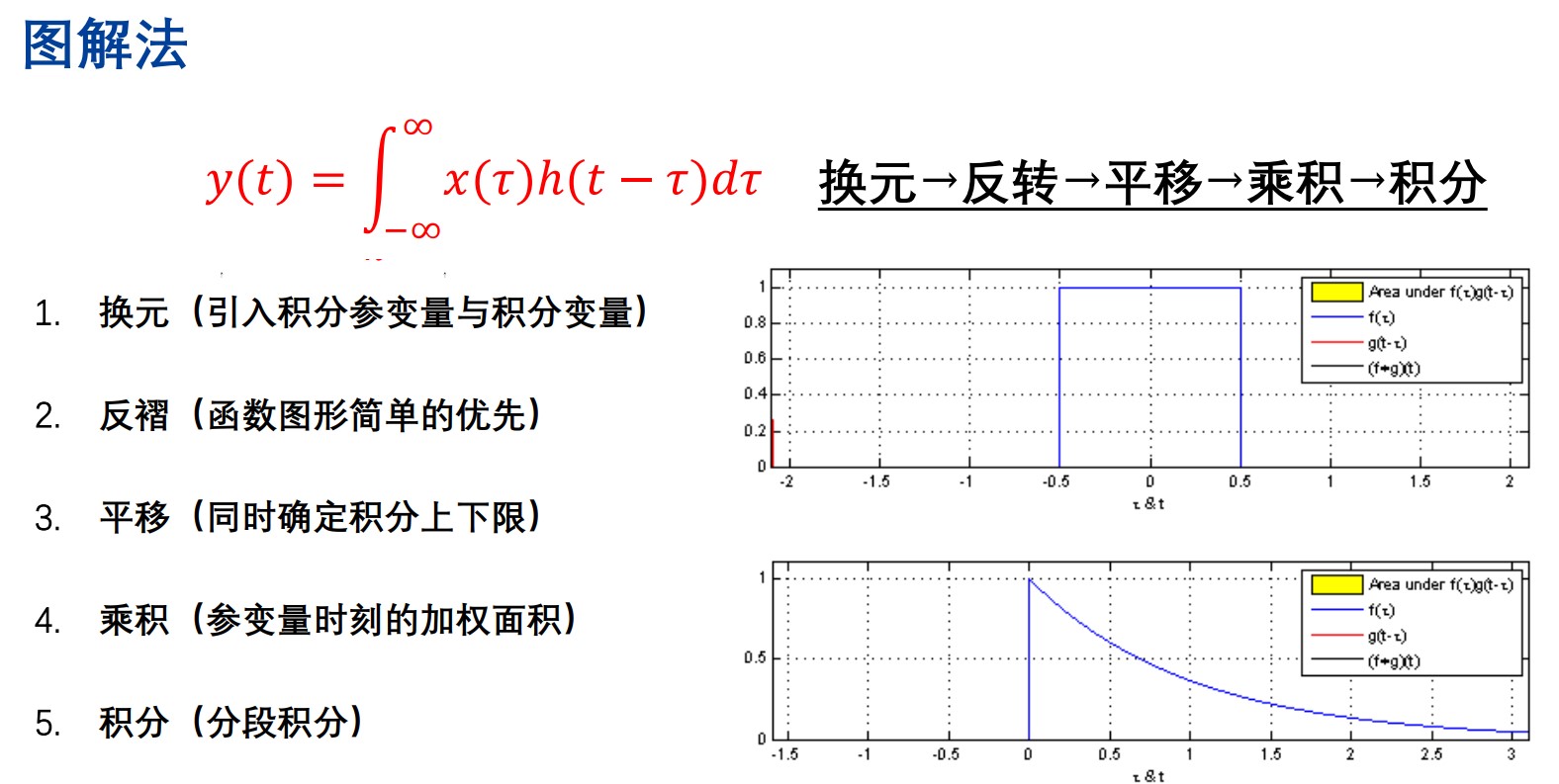
计算卷积积分，可以从上述计算卷积和的类似角度来考虑。值得一提的是图解法：

由于面积是加权面积，所以我们一般考虑将阶跃和常值函数的组合作为固定不动的函数，平移结构比较复杂的那个函数。当然了，能不用作图就不用作图。

卷积的性质⚓︎

卷积的性质对于离散信号和连续信号都成立，只不过表述方式不同而已。下面所述的就不加以区分了。

交换律⚓︎

\[ f_1(t)*f_2(t)=f_2(t)*f_1(t). \]

卷积所代表的“延时加权叠加”中的“权重”与“加权对象”可以对调，但是特定的“权重”与“加权对象”本身可能有固定的物理意义，此时交换可能只有数学意义。

结合律⚓︎

\[ [f_1(t)*f_2(t)]*f_3(t)=f_1(t)*[f_2(t)*f_3(t)]. \]

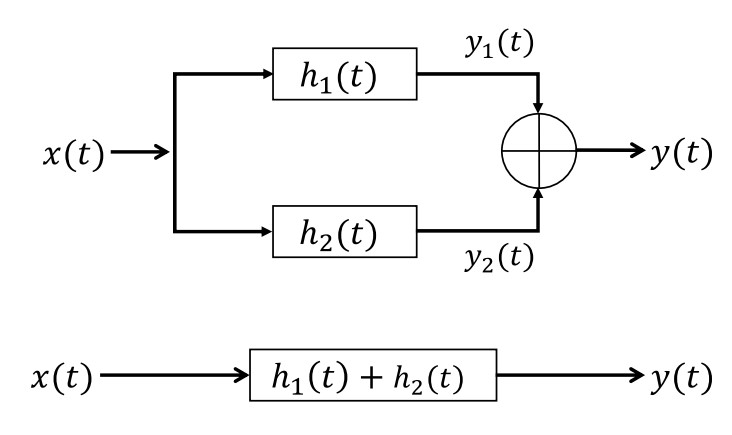
并联LTI系统的单位冲激响应为并联时各个单位冲激响应的和。

卷积的微积分性质⚓︎

若有\(f(t)=f_1(t)*f_2(t)\)，则有：

微分性：

\[ \dfrac{\mathrm{d}f(t)}{\mathrm{d}t}=f_1^\prime(t)*f_2(t)=f_1*f_2(t)^\prime(t). \]

积分性：

\[ \int_{-\infty}^{t}f(\tau)\ \mathrm{d}\tau=f^{(-1)}(t)=f_1^{(-1)}(t)*f_2(t)=f_1*f_2^{(-1)}(t). \]

有始信号的微积分守恒：

\[ f(t)=f_1(t)*f_2(t)=f_1^{(-1)}(t)*f_2^{(1)}(t)=f_1^{(1)}(t)*f_2^{(-1)}(t). \]

奇异函数的卷积性质⚓︎

任何函数与冲激函数的卷积都是其本身：

\[ f(t)*\delta (t)=f(t). \]

任何函数与冲击偶函数的卷积都是其一阶导函数:

\[ f(t)*\delta^\prime(t)=f^\prime (t). \]
\[ f(t)*u(t)=\int_{-\infty}^{t}f(\tau)\ \mathrm{d}\tau. \]

卷积性质的推广⚓︎

时移性质：

\[ f_1(t-t_1)*f_2(t-t_2)=f_1(t-t_2)*f_2(t-t_1). \]

尺度变换：

\[ \left |a\right |f(\dfrac{t}{a})=f_1(\dfrac{t}{a})*f_2(\dfrac{t}{a}). \]

单位冲击响应⚓︎

定义和价值⚓︎

当系统的输入是单位冲击函数\(\delta (t)\)时，系统的输出记作\(h(t)\)，称为单位冲激响应。

对于给定的任意连续输入\(x(t)\)，其响应\(y(t)\)都可以用单位冲激响应来求取：

\[ y(t)=x(t)*h(t). \]

所以，对于给定的系统，只要知道其单位冲激响应，就知道对于任意输入时系统的响应了。

求取单位冲激响应⚓︎

已知描述系统的函数⚓︎

已知描述系统的函数\(g(x(t),y(t))\)的情况下，可以直接令\(x(t)=\delta (t)\)，所求得的结果就是\(h(t)\)。但是，在某些情况下，给定的函数直接做卷积可能并不方便，例如：

\[ y(t)=\int_{-\infty}^{t-2}e^{t-\tau }x(\tau -1)\mathrm{d}\tau. \]

这种情况下，我们可以对积分进行处理，常用手段包括变更积分区间、变量代换。例如：

\[ \begin{aligned} y(t)&=\int_{-\infty}^{t-2}e^{t-\tau }x(\tau -1)\mathrm{d}\tau\\ &=\int_{-\infty}^{+\infty}e^{t-\tau }x(\tau -1)u(t-2-\tau )\mathrm{d}\tau\\ &=\int_{-\infty}^{+\infty}e^{t-\tau^\prime-1 }x(\tau^\prime)u(t-2-\tau^\prime -1 )\mathrm{d}\tau^\prime\\ &=e^{t-1}u(t-3)*x(t). \end{aligned} \]

根据\(y(t)=x(t)*h(t)\)，就可以对比得到\(h(t)\)的表达式了。

已知一组输入输出⚓︎

有些情况下，我们只知道一组对应的输入输出\(x(t),y(t)\)。这种情况下，首先考虑是否能够使用\(x(t)\)及其高阶导函数的线性组合表示出\(\delta (t)\)。若能，则可以使用线性时不变系统的线性性质表达出\(h(t)\)。即若\(\delta (t)\)可以表示成：

\[ \delta (t)=\sum_{k=0}^n c_kx^{(k)}(t), \]

则对应的：

\[ h (t)=\sum_{k=0}^n c_ky^{(k)}(t). \]

系统因果性和稳定性的判据⚓︎

因果性判据⚓︎

对于任意输入\(x(t)\)，由于其输出总是\(x(t)\)与单位冲激响应\(h(t)\)的卷积，故而\(h(t)\)应当蕴含了系统的所有性质。

因果性系统要求单位冲激响应\(h(t)\)满足：\(\forall t<0\)，有\(h(t)=0\)。也就是说，任意时刻输入的任意信号总不会对过去产生影响。

稳定性判据⚓︎

稳定性要求系统对于任意有界的输入，输出也总是有界。这样的系统的单位冲激响应\(h(t)\)满足：\(h(t)\)绝对可积，也就是说：

\[ \int_{-\infty}^{+\infty}\left |h(t)\right |\mathrm{d}t\leqslant A. \]

响应的分类⚓︎

差分方程⚓︎

定义⚓︎

差分方程是微分方程的离散形式。一般形式的差分方程结构如下：

\[ \sum_{k=0}^{M}y[n-k]=\sum_{k=0}^{N}y[n-k]. \]

对于这种方程，我们一般预先知道\(x[n]\)，并且知道\(y[n]\)中的某几项。于是，这样的方程显然就是一种递推方程。

差分方程的齐次解⚓︎

对于一般形式的差分方程，其齐次部分为：

\[ \sum_{k=0}^{M}y[n-k]=0. \]

令\(y[n]\)为特征根的最高次项（\(M\)次方），例如，对于\(ay[n]+by[n-1]+cy[n-2]\)，其特征方程为：

\[ a\lambda ^2+b\lambda +c=0, \]

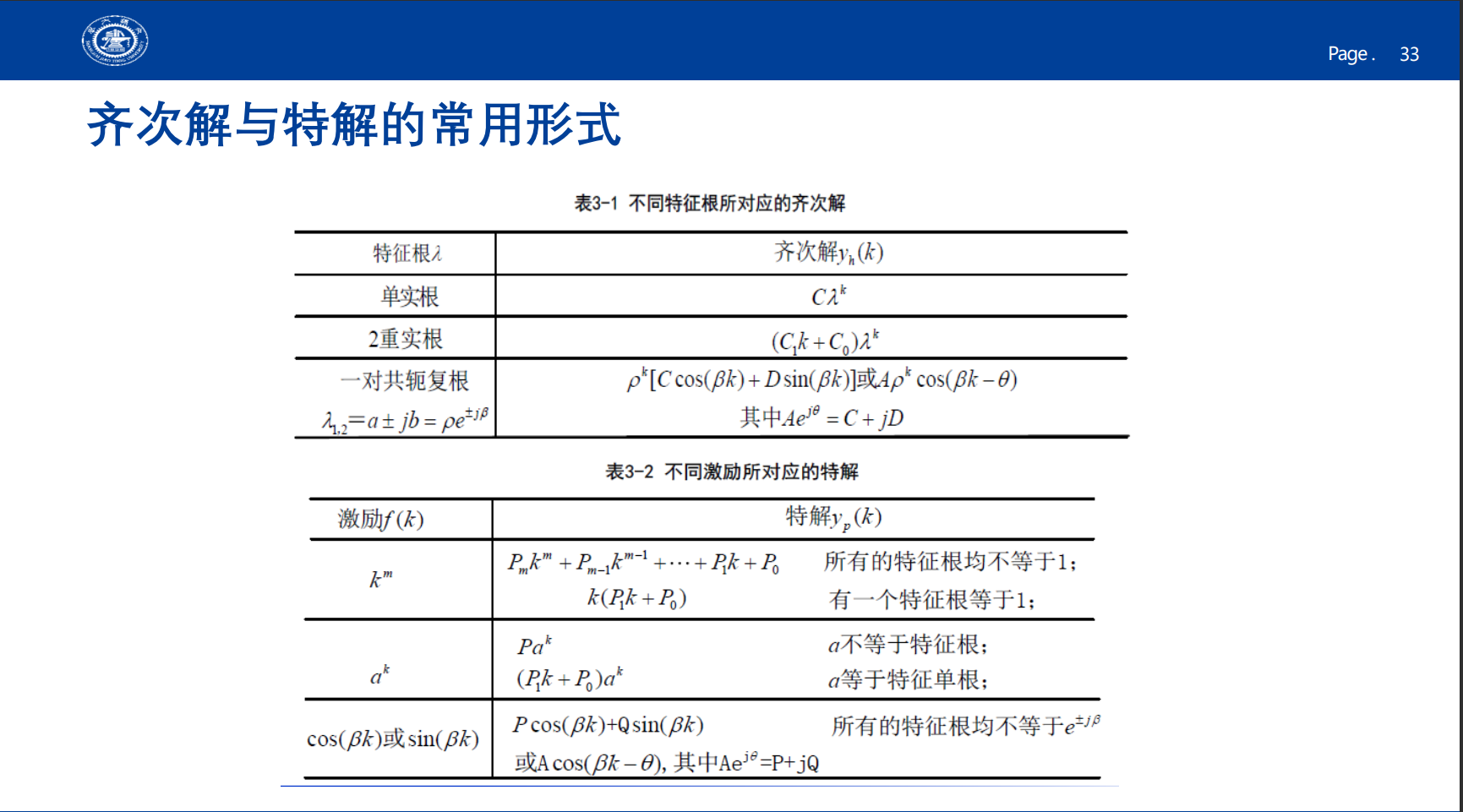
根据其特征根的情况对应写出差分方程齐次部分的待定系数解：

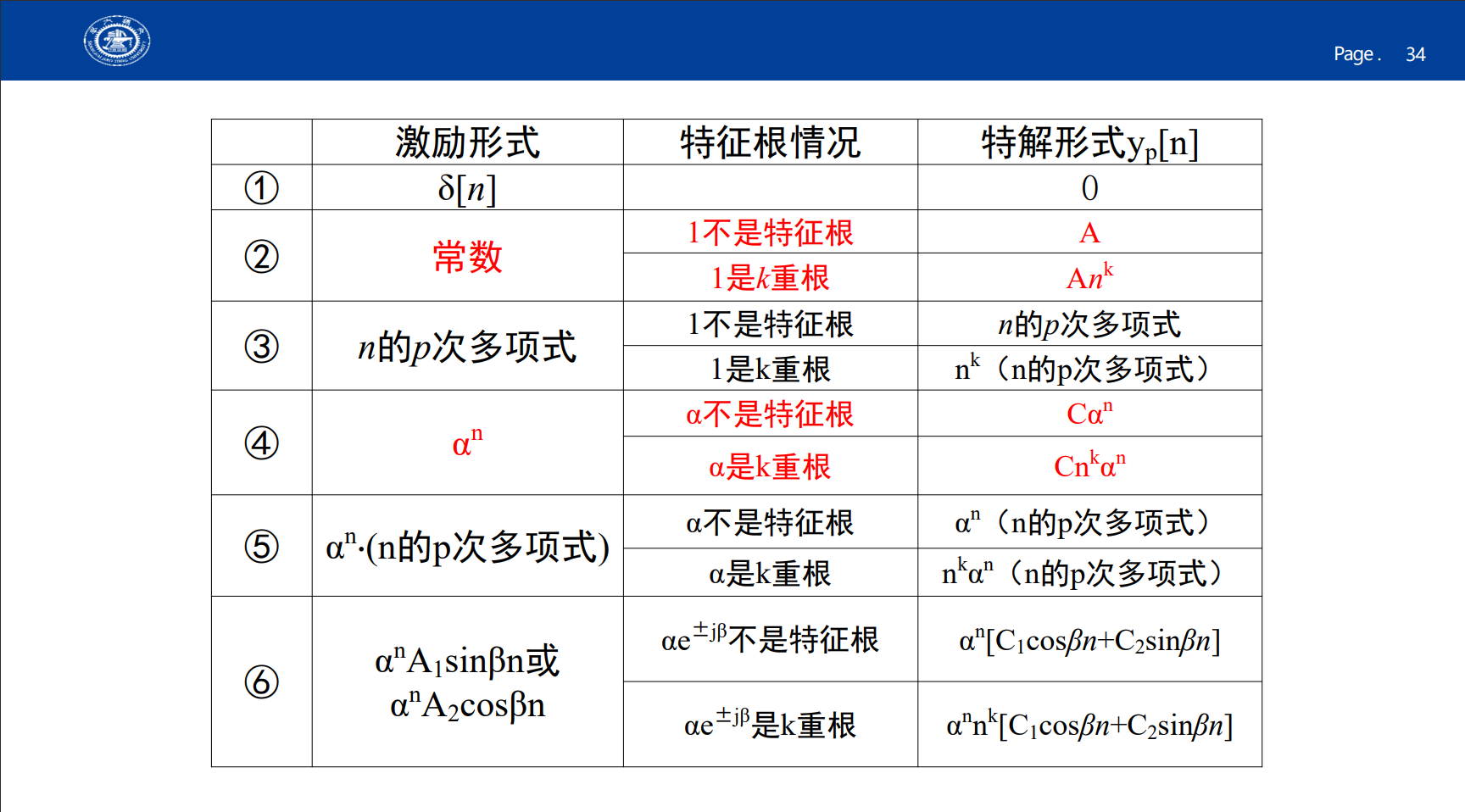
差分方程的特解⚓︎

根据下表，设出特解的一般形式。

于是在\(n\geqslant \max \{M,N\}\)的情况下，带入原差分方程求出特解中的待定系数。

差分方程的全解⚓︎

全解由齐次解和特解一同构成。需要注意的是，由于特解的适用范围为\(n\geqslant \max \{M,N\}\)而非自然数集，故对于\(y[n](n< \max \{M,N\})\)的项需要使用差分方程的递推关系得到。再将这些值作为条件定解出齐次解中仍然含有的待定系数。

最后更新: March 12, 2023
创建日期: March 12, 2023

评论