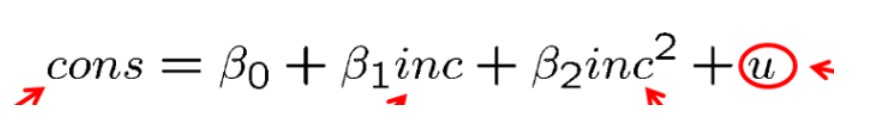跳转至

多元线性回归⚓︎

多元线性回归模型（MLR）⚓︎

定义⚓︎

我们将如下的这种模型定义为多元线性回归模型：

\[ y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_3 + \cdots + \beta_k x_k + u \]

可以看到，多元线性回归模型实际上就是对简单线性回归的一个多元拓展

零条件均值⚓︎

在使用这个模型的时候，我们依然需要假设其满足了零条件均值假设：

\[ E(u|x_1,x_2 \dots x_3) = 0 \]

即扰动项u与所有的自变量都不相关

实际上，由于多元线性回归添加了更多的自变量，考虑了更多的因素，因此多元零状态均值假设实际上更加容易满足

二次项的作用⚓︎

在一元线性回归中，我们已经提到了对数项的作用是表示变化百分比，在此，我们再介绍一下二次项的作用，如下：

二次项在回归模型中的作用是调节边际效应，比如在上式中，如果\(\beta_2\)小于0，则说明随着inc的增大，边际效应逐渐减弱，如果\(\beta_2\)大于0，则说明随着inc的增大，边际效应逐渐增强

最小二乘估计（OLS）⚓︎

针对k元线性回归的模型进行最小二乘估计，即对所有的系数求导，得到k+1个有用的方程并求解

\[ \sum_{i=1}^{n}(y_i - \hat{\beta_0} - \hat{\beta_1}x_{i1} - \hat{\beta_2}x_{i2} ... - \hat{\beta_k}x_{ik})=0 \]
\[ \sum_{i=1}^{n}x_{i1}(y_i - \hat{\beta_0} - \hat{\beta_1}x_{i1} - \hat{\beta_2}x_{i2} ... - \hat{\beta_k}x_{ik})=0 \]
\[ \dots \]
\[ \sum_{i=1}^{n}x_{ik}(y_i - \hat{\beta_0} - \hat{\beta_1}x_{i1} - \hat{\beta_2}x_{i2} ... - \hat{\beta_k}x_{ik})=0 \]

性质⚓︎

\[ \sum_{i=1}^{n}\hat{u_i}=0 \]
\[ \sum_{i=1}^{n}x_{ij}\hat{u_i} = 0 \]
\[ \overline{y} = \hat{\beta_0}+\hat{\beta_1}\overline{x_1}+...+\hat{\beta_k}\overline{x_k} \]

系数的求法——排除干扰⚓︎

在实际使用时，我们往往仅关注一个自变量对因变量的影响，然而实际上，各个自变量之间由于相关性，也会相互干扰，因此我们需要得出一个仅代表目标自变量对因变量影响的系数

完成这一目标应该分为两步： 1. 用兴趣变量向其他自变量做回归（多元回归） 2. 用y对1中的残差做回归（一元回归）

这样做的内在逻辑其实是将\(x_k\)分为\(x_k = \hat{x_k} + \hat{r_k}\)，前一部分代表其余所有变量对此变量的影响，由第一步拟合获得，这样y再对剩下的部分拟合，就能获得\(x_k\)的纯粹影响

这里用一个二元回归举例：

拟合优度⚓︎

同样用

\[ R^2 = \frac{SSE}{SST}=1-\frac{SSR}{SST} \]

作为拟合优度，\(R^2\)越接近于1，拟合效果越好

拟合的统计性质⚓︎

基本假设⚓︎

在讨论拟合的统计性质之前，我们依然做出五条假设： 1. 总体中，y与x线性相关（线性模型的条件） 2. 样本数据随机抽样获得 3. 不存在完全贡献性（不存在成线性关系的两个自变量） 4. 零条件均值 5. \(Var(u_i|x_1,x_2,...,x_k)=\sigma^2\)条件方差为常数

无偏性⚓︎

根据假设1-4，我们可以证明：

\[ E(\hat{\beta_k}|x) = \beta_k \]

即\(\hat{\beta_k}\)是\(\beta_k\)的无偏估计量

变量变化对无偏性的影响⚓︎

假如我们加入一个与y完全无关的变量，估计量的无偏性不会受到影响

这很好理解，因为完全无关，理论上其系数应该为0，而我们可以证明估计量的期望为0，没有违反假设条件，无偏性不受影响

假如我们漏加了一个和y有关的变量，估计量的无偏性可能会产生偏差

我们可以证明其余估计量的期望为

\[ E(\alpha_k|x_k,x) = \beta_k + \beta_l\hat{\delta} \]

其中\(\alpha\)是出错估计中的系数，\(\beta_k\)是理论系数，\(\delta\)是其他参数对未包含参数拟合的残差

我们定义期望与理论值之间的差距为：

\[ Bias(\alpha_k) = \beta_l \hat{\delta} \]

显然，如果漏掉的变量本身对y没有影响的，即\(\beta_l = 0\)；或者其余变量与漏掉的变量都没有关系，即\(\delta = 0\)时，无偏性不受影响

如果Bias不为0，那么应该有如下关系：

方差⚓︎

在假设5的前提下，我们可以得出估计量的方差：

\[ Var(\hat{\beta_j}) = \frac{\sigma^2}{SST_j(1-R_j^2)} \]

和之前一样，如果我们的模型缺少了重要参量，那么方差不再具有无偏性；如果模型多出了某个变量，那么方差的无偏性依然可以保持

方差估计量⚓︎

在之前的种种计算中，我们发现假设5中出现的\(\sigma^2\)是非常关键的量，然而实际上，这个量我们也是没法观测的，只能依靠统计进行估计

我们使用

\[ \hat{\sigma^2} = \frac{1}{n-k-1}\sum_{i=1}^{n} \hat{u_i}^2 \]

作为\(\sigma^2\)的估计量，可以证明，这个估计量是无偏的

最小二乘估计的效果⚓︎

根据高斯-马尔科夫定理：通过OLS得出的估计量的方差是最小的无偏估计量

最后更新: March 12, 2023
创建日期: March 12, 2023

评论