跳转至

简单一元线性回归⚓︎

概率统计回顾⚓︎

基本公式⚓︎

期望的计算：\(E(Y)=\int yf(y)dy\)

条件期望：\(E(Y|X)=\int yf(y|X)dy\)

条件概率密度分布：\(f_{Y|X}(y|x)=f_{X,Y}(x,y)/f_{X}(x)\)

相关系数：\(\rho_{XY}=Cov(X,Y)/\sigma_{X}\sigma_{Y}\)

期望的性质⚓︎

性质1：\(E[g(x)|x]=g(x)\)

性质2：\(E[a(x)y+b(x)|x]=a(x)E(y|x)+b(x)\)

性质3：如果x与y相互独立，则\(E(y|x)=E(y)\)

性质4：\(E[E(y|x)]=E(y)\)

简单线性回归模型⚓︎

定义⚓︎

简单线性回归模型被定义为如下形式：

\[ y = \beta_0 + \beta_1 x + u \]

其中，x是自变量，y是因变量，u是误差项

误差项包括除了x以外所有可能对y产生影响的因素

从上述分析中我们不难看出，如果u和x无关，那么\(\beta_1\)就可以表示x变化一单位时，y的变化量。当然，现实不总是这样的美好，很多时候，这样的要求没法实现

零条件均值假设（Zero Conditional Mean Assumption）⚓︎

定义⚓︎

如果\(E(u|x)\)对任何x都成立，那么我们说简单线性回归模型满足零条件均值假设，即：

\[ E(u|x)=0 \]

首先要说明的是：零条件均值假设是一个比线性无关强，但是比相互独立弱的条件，即：

若\(E(u|x)=0\) , 则\(cov(x,u)=0\)，但u和x不一定相互独立

性质⚓︎

如果零条件均值假设成立，那么以下表述成立：

\[ E(E(u|x))=E(u)=0 \]
\[ E(g(x)u|x)=g(x)E(u|x)=0 \]
\[ E[E(g(x)u|x)]=E(g(x)u)=0 \]
\[ cov(g(x),u)=0 \]

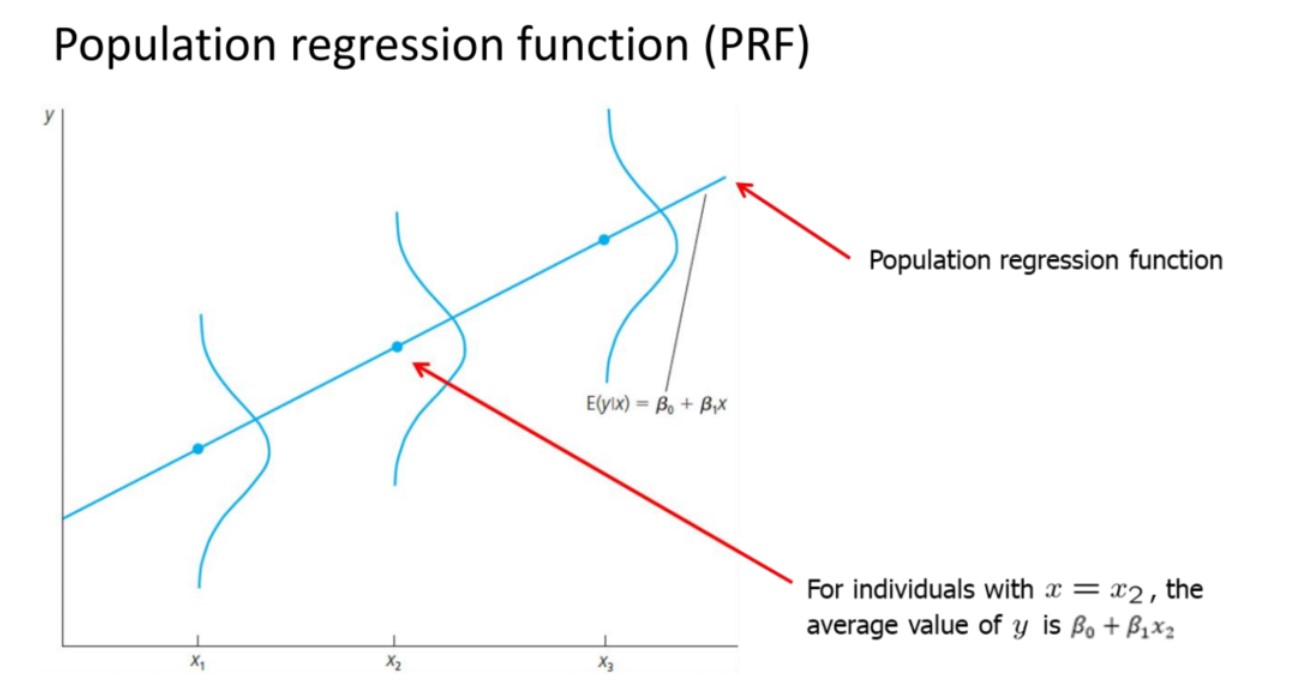
总体回归函数（PRF）⚓︎

虽然零条件均值假设是一种假设，但是其在分析中具有一定的实际意义，现在，让我们将这条假设运用于简单线性回归模型中

\[ y=\beta_0 + \beta_1 x + u \]
\[ E(y|x)=E((\beta_0 + \beta_1 x + u)|x) \]
\[ E(y|x)=\beta_0+\beta_1x+E(u|x) \]
\[ E(y|x)=\beta_0+\beta_1x \]

从上述分析中，我们知道：

对于每一个特定的x值，y在此x下分布的均值应该是\(\beta_0 + \beta_1 x\)，下图可以更清晰的显示这一结论：

最小二乘法计算回归模型⚓︎

对于回归模型：

\[ y = \beta_0 + \beta_1 x + u \]

如果想要求出\(\beta_0\)和\(\beta_1\)，显然，我们需要测量若干组\((x_i,y_i)\)

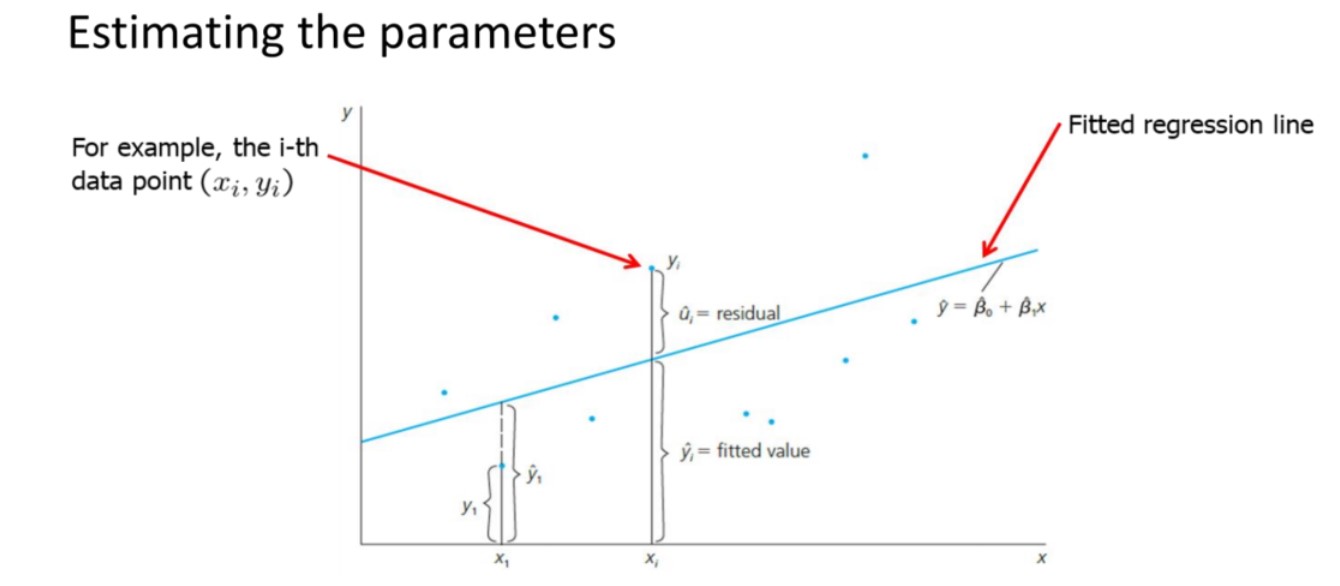
当我们拥有了这些数据之后，我们应该有一条标准来衡量怎样的直线能最好的反映这些数据的线性关系，如下图所示：

我们假设需要找的直线是:\(\hat{y}=\hat{\beta_0}+\hat{\beta_1}x\)

并将残差定义为:\(\hat{u_i}=y_i-\hat{y_i}\)

依据最小二乘估计，我们要保证所有\(\hat{u_i}\)的平方和最小，即

\[ min_{b_0,b_1}\sum_{i=1}^{n}(y_i-b_0-b_1x_i)^2 \]

利用求导运算和极值条件，有：

\[ 2\sum_{i=1}^{n}(y_i-\hat{\beta_0}-\hat{\beta_1}x_i)=0 \quad (FOC1) \]
\[ 2\sum_{i=1}^{n}x_i(y_i-\hat{\beta_0}-\hat{\beta_1}x_i)=0 \quad (FOC2) \]

这样，我们得到：

\[ \hat{\beta_1}=\frac{\sum_{i=1}^{n}(x_i-\overline{x})(\hat{y_i}-\overline{y})}{\sum_{i=1}^{n}(x_i-\overline{x})^2}=\frac{\sum x_i \sum y_i - \sum{x_iy_i}}{(\sum{x_i})^2-\sum{x_i^2}} \]
\[ \hat{\beta_0}=\overline{y}-\hat{\beta_1}\overline{x} \]

我们将\(\hat{y}=\hat{\beta_0}+\hat{\beta_1}\hat{x}\)称为样本回归模型（SRF）

对方差分析（ANOVA）⚓︎

定义⚓︎

对于每一个实际的样本点，可以做如下分解：

\[ y_i = \hat{y_i}+\hat{u_i} \]

针对这一分解，我们做如下定义：

SST(total Sum of Squares):\(\sum{(y_i-\overline{y_i})^2}\)

SSE(Explained Sum of Squares):\(\sum{(\hat{y_i}-\overline{y_i})^2}\)

SSR(Residual Sum of Squares):\(\sum{\hat{u_i}^2}\)

可以证明ANOVA结论：

\[ SST = SSE + SSR \]

拟合优度⚓︎

定义：

\[ R^2 = \frac{SSE}{SST}=1-\frac{SSR}{SST} \]

为拟合优度，\(R^2\)越接近于1，拟合效果越好

不同形式的简单线性回归⚓︎

除了线性对线性的最一般的简单线性回归模型，我们通过改变自变量的形式，还能产生两种常见的有意义的模型

log-line形式⚓︎

满足

\[ log(y) = \beta_0 + \beta_1 x \]

这个模型表示：随自变量每变化一单位，因变量变化固定的百分比

log-log形式⚓︎

满足

\[ log(y) = \beta_0 + \beta_1 log(x) \]

这个模型表示：随着自变量没变化一百分比，因变量变化固定百分比

这个模型在意义上，与经济学原理中“弹性”的概念非常相似

总结一下，不难看出，不加log反映的是值本身的变化，加了log之后反映的是百分比的变化

统计量的统计学性质⚓︎

在简单线性回归模型中，我们计算了\(\hat{\beta_0}\)和\(\hat{\beta_1}\)，实际上，由于样本的选取是随机的，而这两个统计量取决于样本，因此，\(\hat{\beta_0}\)和\(\hat{\beta_1}\)本质上也是两个随机变量 既然是随机变量，那么我们就希望能够找到他们的统计学性质，比如他们的期望和方差

基本假设⚓︎

在讨论问题之前，我们有必要对条件进行一些假设，来缩小问题的范围，这里我们做5条假设： 1. 总体中，y与x线性相关（线性模型的条件） 2. 样本数据随机抽样获得 3. 随机样本方差大于0（样本不全都相等） 4. 零条件均值 5. \(Var(u_i|x_i)=\sigma^2\)条件方差为常数

期望——无偏性⚓︎

根据之前的假设，我们可以证明：

\[ E(\hat{\beta_0}) = \beta_0 \]
\[ E(\hat{\beta_1}) = \beta_1 \]

即，\(\hat{\beta_0}\)和\(\hat{\beta_1}\)是\(\beta_0\)和\(\beta_1\)的无偏估计量

这说明，在平均意义上，我们求出的参数就能代表实际的参数，依据大数定理，如果样本容量足够，那么其均值将在数学意义上等于实际值

方差⚓︎

方差的意义在于，在我们已知\(\hat{\beta_0}\)和\(\hat{\beta_1}\)无偏的条件下，如果方差较小，那么可以想象，\(\hat{\beta_0}\)和\(\hat{\beta_1}\)应该在实际值周围很小的区域内波动，那么样本求出的值就可以很好的拟合真实值

经过计算，可以得出

\[ Var(\hat{\beta_1})=\frac{\sigma^2}{SST_x} \]
\[ Var(\hat{\beta_0})=\frac{\sigma^2 n^{-1}\sum_{i=1}^{n}x_i^2}{SST_x} \]

在此，我们对\(\hat{\beta_1}\)的值做一些解释，可以看出，他正比与u的方差而反比于x的方差，这是合理的：u的方差越大，表示误差分布的越散，在图上表现出来的就是拟合直线的斜率可以在更大的范围内选择，斜率方差变大；x的方差越大，说明抽样点分布的越散，就有更多的极端情况被采样到，准确性提高，对y的估计更好，斜率方差变小

对\(\sigma^2\)的估计方式⚓︎

在之前的种种计算中，我们发现假设5中出现的\(\sigma^2\)是非常关键的量，然而实际上，这个量我们也是没法观测的，只能依靠统计进行估计

我们使用

\[ \hat{\sigma^2} = \frac{1}{n-2}\sum_{i=1}^{n} \hat{u_i}^2 \]

作为\(\sigma^2\)的估计量

不难证明，这个估计量对于\(\sigma^2\)是无偏的

在此基础上，我们就找到了估计\(\hat{\beta_0}\)和\(\hat{\beta_1}\)方差的方法，即：

\[ Var(\hat{\beta_1})=\frac{\hat{\sigma^2}}{SST_x} \]
\[ Var(\hat{\beta_0})=\frac{\hat{\sigma^2} n^{-1}\sum_{i=1}^{n}x_i^2}{SST_x} \]
最后更新: March 12, 2023
创建日期: March 12, 2023

评论